Quaternion group
A metabelian  -group (cf. Meta-Abelian group) of order 8, defined by generators
-group (cf. Meta-Abelian group) of order 8, defined by generators  and relations
and relations
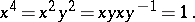 |
The quaternion group can be isomorphically imbedded in the multiplicative group of the algebra of quaternions (cf. Quaternion; the imbedding is defined by the relation 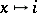 ,
, 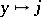 ). The assignment
). The assignment
 |
defines a faithful representation of the quaternion group by complex 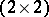 -matrices.
-matrices.
A generalized quaternion group (a special case of which is the quaternion group for 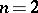 ) is a group defined on generators
) is a group defined on generators  and
and 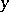 and relations
and relations
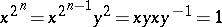 |
(where  is a fixed number). The group is a
is a fixed number). The group is a  -group of order
-group of order  and nilpotency class
and nilpotency class  .
.
The quaternion group is a Hamilton group, and the minimal Hamilton group in the sense that any non-Abelian Hamilton group contains a subgroup isomorphic to the quaternion group. The intersection of all non-trivial subgroups of the quaternion group (and also of any generalized quaternion group) is a non-trivial subgroup. Every non-Abelian finite group with this property is a generalized quaternion group. Among the finite Abelian groups, only the cyclic 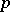 -groups (cf.
-groups (cf. 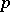 -group; Cyclic group) have this property. The generalized quaternion groups and the cyclic
-group; Cyclic group) have this property. The generalized quaternion groups and the cyclic 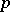 -groups are the only
-groups are the only  -groups admitting a proper
-groups admitting a proper  -homomorphism, that is, a homomorphism of the lattice of subgroups onto some lattice
-homomorphism, that is, a homomorphism of the lattice of subgroups onto some lattice 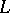 that is not an isomorphism.
that is not an isomorphism.
Sometimes the term "quaternion group" is used to denote various subgroups of the multiplicative group of the algebra of quaternions and related topological groups.
References
| [1] | M. Hall jr., "Group theory" , Macmillan (1959) |
Comments
The imbedding 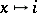 ,
,  of the quaternion group
of the quaternion group 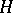 into the quaternion algebra gives a surjective algebra homomorphism of the group algebra
into the quaternion algebra gives a surjective algebra homomorphism of the group algebra 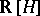 to the quaternion algebra, exhibiting the latter as the quotient of
to the quaternion algebra, exhibiting the latter as the quotient of  by the ideal
by the ideal 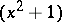 .
.
Quaternion group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quaternion_group&oldid=32679