Hardy transform
From Encyclopedia of Mathematics
The integral transform
 |
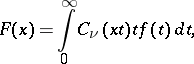where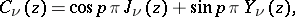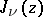
 |
and 
and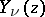 
are the Bessel functions of the first and second kinds, respectively. For 
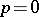the Hardy transform coincides with one of the forms of the Hankel transform, and for 
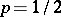with the 
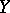-transform. The Hardy transform was proposed by G.H. Hardy in [1].
The inversion formula is
 |
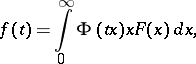where
 |
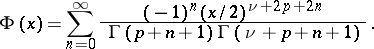The Hardy transform is also defined for certain classes of generalized functions.
References
| [1] | G.H. Hardy, "Some formulae in the theory of Bessel functions" Proc. London. Math. Soc. (2) , 23 (1925) pp. 61–63 |
| [2] | Y.A. Brychkov, A.P. Prudnikov, "Integral transforms of generalized functions" , Gordon & Breach (1989) (Translated from Russian) |
How to Cite This Entry:
Hardy transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_transform&oldid=32672
Hardy transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_transform&oldid=32672
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article