Betti group

In a broad sense, the same as a homology group; in a narrow sense, the Betti group is the free part of the homology group with as domain of coefficients the group 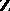of integers, if this homology group is finitely generated. Named after E. Betti (1823–1892).

References

[1]	H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German)
[2]	P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian)

References

[a1]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966)