Cap

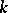-cap

A set of 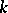points of a finite projective space 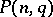no three of which are collinear. Two caps are considered equivalent if there is a collineation of 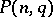transforming one into the other. The search for the maximal number 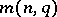of points of a cap in 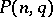, the construction, and the classification of 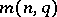-caps form important problems in the study of caps that are not yet (1984) completely solved. The following results are known (see [2], [3]):

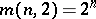; the 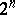-cap is unique (up to equivalence) and is a set of points not located in a fixed hyperplane in ;

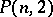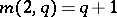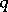if is odd; the 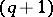-cap in 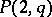is unique and is a conic;

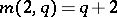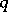if is even; a 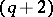-cap in 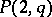is, generally speaking, not unique;

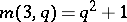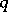. If is odd the 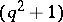-cap in 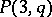is unique and is an elliptic quadric; if 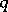is even it is, generally speaking, not unique;

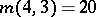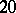; a -cap in 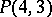is not unique;

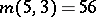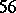; the -cap in 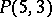is unique.

Caps are used in coding theory (cf., e.g., [2]).

References

[1]	R.C. Bose, "Mathematical theory of the symmetrical factorial design" Shankhyā , 8 (1947) pp. 107–166
[2]	R. Hill, "Caps and codes" Discrete Math. , 22 : 2 (1978) pp. 111–137
[3]	B. Segre, "Introduction to Galois geometries" Atti Accad. Naz. Lincei Mem. , 8 (1967) pp. 133–236

Comments

In the (differential) topology of surfaces a cap of the second kind or cross cap is a -dimensional manifold with boundary homeomorphic to the Möbius strip used to construct (more complicated) surfaces by removing a disc and replacing it with a cross cap or with a bundle (also called a cap of the first kind). Cf. Theory of surfaces for more details.