Noetherian induction
A reasoning principle applicable to a partially ordered set in which every non-empty subset contains a minimal element; for example, the set of closed subsets in some Noetherian space. Let 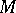 be such a set and let
be such a set and let 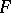 be a subset of it having the property that for every
be a subset of it having the property that for every 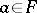 there is a strictly smaller element
there is a strictly smaller element 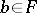 . Then
. Then 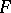 is empty. For example, let
is empty. For example, let 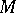 be the set of all closed subsets of a Noetherian space and let
be the set of all closed subsets of a Noetherian space and let 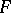 be the set of those closed subsets that cannot be represented as a finite union of irreducible components. If
be the set of those closed subsets that cannot be represented as a finite union of irreducible components. If 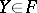 , then
, then 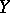 is reducible, that is,
is reducible, that is, 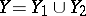 , where
, where  and
and 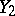 are closed, both are strictly contained in
are closed, both are strictly contained in 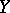 and at least one of them belongs to
and at least one of them belongs to 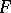 . Consequently,
. Consequently, 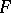 is empty.
is empty.
Reversal of the order makes it possible to apply Noetherian induction to partially ordered sets in which every non-empty subset contains a maximal element; for example, to the lattice of ideals in a Noetherian ring.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Comments
The term well-founded induction is also in use.
Noetherian induction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Noetherian_induction&oldid=32633