Isolated subgroup
A subgroup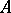 
of a group 
such that 
whenever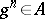 
, 
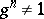; in other words, if an equation 
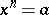(where 
) is solvable in 
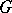, then the solution lies in 
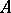. A subgroup 
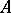is said to be strongly isolated if for every 
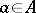the centralizer of 
in the whole group lies in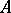 
. The isolator of a set 
of elements of a group is the smallest isolated subgroup containing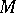 
.
In an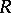 
-group (that is, in a group with unique division), the concept of an isolated subgroup corresponds to that of a pure subgroup of an Abelian group. The intersection of isolated subgroups in an 
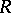-group is an isolated subgroup. A normal subgroup 
of an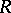 
-group 
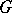is isolated if and only if the quotient group 
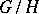is torsion-free. The centre of an 
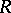-group is isolated.
In the theory of ordered groups, isolated subgroups are sometimes referred to as convex subgroups (cf. Convex subgroup).
Comments
References
| [a1] | A.G. Kurosh, "Theory of groups" , 2 , Chelsea (1960) pp. §66 (Translated from Russian) |
Isolated subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isolated_subgroup&oldid=32631