Centre of a partially ordered set
From Encyclopedia of Mathematics
The set of elements of a partially ordered set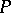 
with a 0 and a 1 (in particular, of a lattice) for which in some decomposition of 
into a direct product one of the components is 1 and the other is 0. The centre of any partially ordered set with a 0 and a 1 is a Boolean algebra. An element 
of a lattice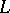 
belongs to the centre if and only if it is neutral (that is, if every triple of elements 
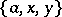generates a distributive sublattice of 
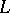) and has a complement. In a complemented modular lattice the centre coincides with the set of all elements having a unique complement.
How to Cite This Entry:
Centre of a partially ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Centre_of_a_partially_ordered_set&oldid=32614
Centre of a partially ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Centre_of_a_partially_ordered_set&oldid=32614
This article was adapted from an original article by T.S. Fofanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article