Thermal-conductance equation

heat equation

The homogeneous partial differential equation

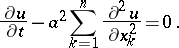This equation is the simplest example of a parabolic partial differential equation. For it describes the process of heat diffusion in a solid body. The first boundary value problem (in a cylindrical domain) and the Cauchy–Dirichlet problem (in a half-space) are the fundamental well-posed problems for the thermal-conductance equation. A solution to the characteristic (Cauchy) problem can be given in explicit form:

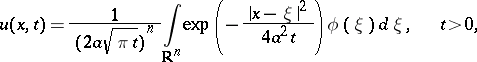where 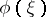is a fixed continuous uniformly bounded function on .

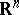References

[1]	A.V. Bitsadze, "The equations of mathematical physics" , MIR (1980) (Translated from Russian)
[2]	V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian)

References

[a1]	J.R. Cannon, "The one-dimensional heat equation" , Addison-Wesley (1984)
[a2]	H.S. Carslaw, J.C. Jaeger, "Conduction of heat in solids" , Clarendon Press (1945)
[a3]	J. Cranck, "The mathematics of diffusion" , Clarendon Press (1975)
[a4]	A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964)
[a5]	M. Jakob, "Heat transfer" , 1–2 , Wiley (1975)
[a6]	M.N. Ozisik, "Basic heat transfer" , McGraw-Hill (1977)
[a7]	D.V. Widder, "The heat equation" , Acad. Press (1975)