Gauss variational problem

A variational problem, first studied by C.F. Gauss (1840) [1], which may be formulated in modern terms as follows. Let 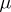be a positive measure in a Euclidean space 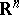, , 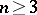of finite energy (cf. Energy of measures), and let

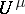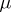define the Newton potential of . Out of all measures with compact support 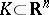it is required to find a measure 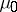giving the minimum of the integral

which is the scalar product (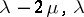) in the pre-Hilbert space of measures of finite energy.

The importance of the Gauss variational problem consists in the fact that the equilibrium measure (cf. Robin problem) may be obtained as a solution of the Gauss variational problem for a certain choice of 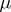; for example, may be taken to be a homogeneous mass distribution over a sphere with centre in the coordinate origin that includes .

References

[1]	C.F. Gauss, "Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehung- und Abstössungs-Kräfte" , Werke , 5 , K. Gesellschaft Wissenschaft. Göttingen (1877) pp. 195–242
[2]	N.S. [N.S. Landkov] Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian)
[3]	M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959)

Comments

The measure 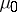is the projection of on the convex cone of all positive measures , of finite energy, and with support contained in . See also [a1], Chapt. I.XIII for a treatment of this subject.

References

[a1]	J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984)