Oblique derivative
From Encyclopedia of Mathematics
directional derivative
A derivative of a function 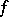 defined in a neighbourhood of the points of some surface
defined in a neighbourhood of the points of some surface 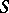 , with respect to a direction
, with respect to a direction 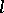 different from the direction of the conormal of some elliptic operator at the points of
different from the direction of the conormal of some elliptic operator at the points of 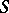 . Oblique derivatives may figure in the boundary conditions of boundary value problems for second-order elliptic equations. The problem is then called a problem with oblique derivative. See Differential equation, partial, oblique derivatives.
. Oblique derivatives may figure in the boundary conditions of boundary value problems for second-order elliptic equations. The problem is then called a problem with oblique derivative. See Differential equation, partial, oblique derivatives.
If the direction field 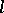 on
on 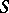 has the form
has the form 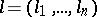 , where
, where 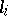 are functions of the points
are functions of the points 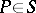 such that
such that 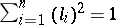 , then the oblique derivative of a function
, then the oblique derivative of a function 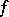 with respect to
with respect to 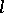 is
is
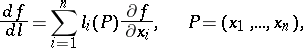 |
where  are Cartesian coordinates in the Euclidean space
are Cartesian coordinates in the Euclidean space 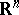 .
.
References
| [1] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
How to Cite This Entry:
Oblique derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oblique_derivative&oldid=32599
Oblique derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oblique_derivative&oldid=32599
This article was adapted from an original article by A.I. Yanushauskas (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article