Convex sets, linear space of

A space whose elements are equivalence classes of pairs of convex sets (cf. Convex set) in a locally convex linear topological space. The pair 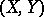is treated as the "difference" 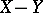, pairs 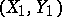and being equivalent by definition if , where addition of sets is understood to mean the closure of the vector sum. Addition, subtraction, multiplication by a scalar, and a topology are introduced in the space of convex sets, that space becoming thereby a locally convex topological space. Also the concept of partial ordering is introduced, which is analogous to inclusion of sets. Linear spaces of convex sets are also considered in non-locally convex linear spaces.

References

[1]	A.G. Pinsker, "The space of convex sets of a locally convex space" Trudy Leningrad. Inzh.-Ekon. Inst. , 63 (1966) pp. 13–17 (In Russian)