Rouché theorem
Let  and
and  be regular analytic functions (cf. Analytic function) of a complex variable
be regular analytic functions (cf. Analytic function) of a complex variable  in a domain
in a domain 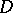 , let a simple closed piecewise-smooth curve
, let a simple closed piecewise-smooth curve 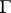 together with the domain
together with the domain 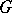 bounded by it belong to
bounded by it belong to  and let everywhere on
and let everywhere on  the inequality
the inequality 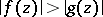 be valid; then in the domain
be valid; then in the domain 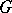 the sum
the sum 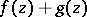 has the same number of zeros as
has the same number of zeros as 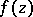 .
.
This theorem was obtained by E. Rouché [1]. It is a corollary of the principle of the argument (cf. Argument, principle of the) and it implies the fundamental theorem of algebra for polynomials.
A generalization of Rouché's theorem for multi-dimensional holomorphic mappings is also valid, for example, in the following form. Let 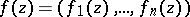 and
and  be holomorphic mappings (cf. Analytic mapping) of a domain
be holomorphic mappings (cf. Analytic mapping) of a domain 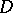 of the complex space
of the complex space 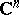 into
into 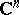 ,
, 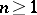 , with isolated zeros, let a smooth surface
, with isolated zeros, let a smooth surface 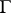 homeomorphic to the sphere belong to
homeomorphic to the sphere belong to 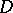 together with the domain
together with the domain 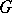 bounded by it and let the following inequality hold on
bounded by it and let the following inequality hold on 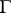 :
:
 |
Then the mapping 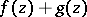 has in
has in  the same number of zeros as
the same number of zeros as  .
.
References
| [1] | E. Rouché, J. Ecole Polytechn. , 21 (1858) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
There is a symmetric form of Rouché's theorem, which says that if 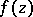 and
and 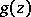 are analytic and satisfy the inequality
are analytic and satisfy the inequality 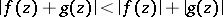 on
on 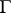 , then
, then  and
and 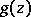 have the same number of zeros inside
have the same number of zeros inside 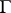 . See [a2]–[a3] for generalizations of Rouché's theorem in one variable; see [a1] for the case of several variables.
. See [a2]–[a3] for generalizations of Rouché's theorem in one variable; see [a1] for the case of several variables.
References
| [a1] | L.A. Aizenberg, A.P. Yuzhakov, "Integral representations and residues in multidimensional complex analysis" , Transl. Math. Monogr. , 58 , Amer. Math. Soc. (1983) (Translated from Russian) |
| [a2] | R.B. Burchel, "An introduction to classical complex analysis" , 1 , Acad. Press (1979) |
| [a3] | J.B. Conway, "Functions of one complex variable" , Springer (1978) |
Rouché theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rouch%C3%A9_theorem&oldid=32579