Skew Young tableau
Consider two partitions,  of
of 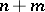 and
and 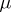 of
of 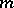 . With those partitions one can associate Young diagrams, or Ferrers diagrams (cf. Young diagram), also denoted by
. With those partitions one can associate Young diagrams, or Ferrers diagrams (cf. Young diagram), also denoted by 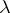 and
and 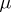 . Suppose that each cell of
. Suppose that each cell of 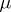 is also a cell of
is also a cell of 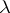 . The set-difference
. The set-difference 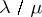 contains exactly
contains exactly  cells. It is called a skew Young diagram, or skew Ferrers diagram.
cells. It is called a skew Young diagram, or skew Ferrers diagram.
Such a diagram can be filled with integers from 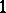 to
to  in increasing order in each row and in each column. This is called a standard skew Young tableau. If repetitions are allowed and if the rows are only non-decreasing, the tableau is called semi-standard. These are generalizations of Young tableaux (cf. Young tableau).
in increasing order in each row and in each column. This is called a standard skew Young tableau. If repetitions are allowed and if the rows are only non-decreasing, the tableau is called semi-standard. These are generalizations of Young tableaux (cf. Young tableau).
For example,
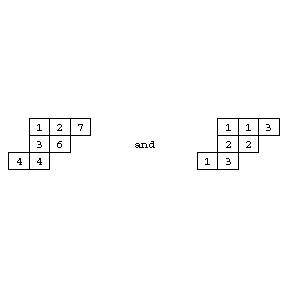
Figure: s110150a
are standard, respectively semi-standard, of shape 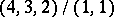 .
.
It is possible to define the Schur function 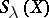 combinatorially as the generating function of all semi-standard Young tableaux of shape
combinatorially as the generating function of all semi-standard Young tableaux of shape 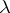 filled with indices of elements of
filled with indices of elements of 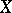 , as follows.
, as follows.
Let  be an alphabet. Let
be an alphabet. Let 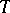 be a semi-standard Young tableau of shape
be a semi-standard Young tableau of shape 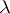 , containing entries from
, containing entries from 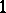 to
to 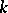 . The product of the indeterminates whose indices appear in
. The product of the indeterminates whose indices appear in 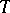 is a monomial. Then
is a monomial. Then 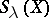 is the sum of those monomials over the set of all possible such tableaux
is the sum of those monomials over the set of all possible such tableaux 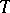 .
.
When replacing Young tableaux by skew Young tableaux of shape 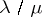 , one obtains the skew Schur function
, one obtains the skew Schur function 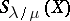 . Those functions have many properties in common with ordinary Schur functions. See [a3] for Schur functions.
. Those functions have many properties in common with ordinary Schur functions. See [a3] for Schur functions.
This connection between combinatorial (Young tableaux) and algebraic (Schur functions) objects is very fruitful, both for combinatorics and for algebra. For applications to 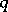 -analysis, cf., e.g., [a1] and [a2].
-analysis, cf., e.g., [a1] and [a2].
References
| [a1] | J. Désarménien, "Fonctions symétriques associées à des suites classiques de nombres" Ann. Sci. Ecole Normale Sup. , 16 (1983) pp. 231–304 |
| [a2] | J. Désarménien, D. Foata, "Fonctions symétriques et séries hypergéométriques basiques multivariées" Bull. Soc. Math. France , 113 (1985) pp. 3–22 |
| [a3] | I.G. Macdonald, "Symmetric functions and Hall polynomials" , Clarendon Press (1995) (Edition: Second) |
Skew Young tableau. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skew_Young_tableau&oldid=32569