Star-like function

univalent star-like function

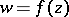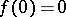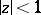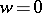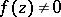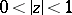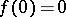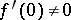A function which is regular and univalent in the disc , , and maps onto a star-like domain with respect to . A function , in , , , regular in 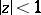, is star-like in this disc if and only if it satisfies the condition

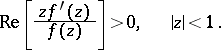The family of star-like functions in 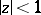, normalized so that 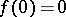, , 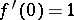forms the class 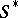, which admits a parametric representation by Stieltjes integrals:

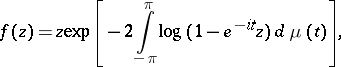where 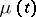is a non-decreasing function on , .

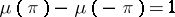For the class 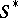the coefficient problem has been solved; sharp estimates have been found for 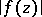, , 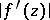, 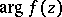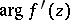(the argument of the function is the branch that vanishes at 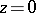). The extremal functions for these estimates are 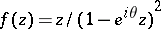, where 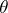is real. The class 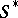of functions 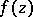is related to the class of functions 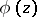, , 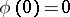, 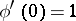that are regular and univalent in 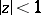and map 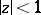onto a convex domain, by the formula .

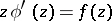A star-like function such that

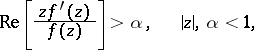is called a star-like function of order 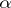in .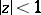

Attention has also been given to univalent star-like functions in an annulus (see [1]), 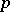-valent star-like functions and weakly star-like functions in a disc (see [2], [4]), -locally star-like functions (see [1]), and functions which are star-like in the direction of the real axis (see [3]). For star-like functions of several complex variables, see [5].

References

[1]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[2]	J.A. Hummel, "Multivalent starlike functions" J. d'Anal. Math. , 18 (1967) pp. 133–160
[3]	M.S. Robertson, "Analytic functions star-like in one direction" Amer. J. Math. , 58 : 3 (1936) pp. 465–472
[4]	A.W. Goodman, "Open problems on univalent and mutivalent functions" Bull. Amer. Math. Soc. , 74 : 6 (1968) pp. 1035–1050
[5]	I.I. Bavrin, "Classes of holomorphic functions of several complex variables and extremal problems for these classes of functions" , Moscow (1976) (In Russian)

References

[a1]	A.W. Goodman, "Univalent functions" , 1 , Mariner (1983)
[a2]	P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11
[a3]	C. Pommerenke, "Univalent functions" , Vandenhoeck & Ruprecht (1975)