Star-like domain
with respect to a fixed point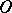 
A domain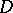 
in the complex space 
, 
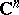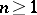, such that, for any point of 
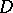, the segment of the straight line from that point to 
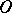lies entirely in 
.
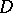A simply-connected open Riemann surface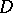 
over the 
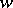-plane is called a 
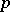-sheeted star-like domain with respect to a fixed point 
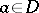(where 
is a natural number) if there exist 
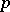points of 
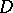above 
(counting multiplicities) and if, for any point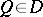 
, there is a path 
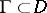from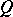 
to one of the points above 
such that the projection of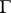 
on the 
-plane is the straight-line segment joining the projection of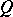 
to 
.
Let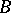 
be a doubly-connected domain in the 
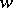-plane, let 
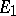and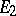 
be complementary continua, 
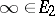, let 
be a fixed point of 
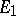, and let 
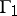and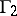 
be the boundary components of 
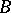. Then 
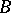is said to be star-like with respect to 
if either each of the simply-connected domains containing 
and bounded by 
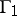and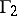 
is star-like, or 
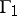is the union of the straight-line segments issuing from 
and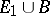 
is star-like with respect to 
.
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | J.A. Hummel, "Multivalent starlike functions" J. d'Anal. Math. , 18 (1967) pp. 133–160 |
Comments
For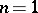 
, star-like domains are the images of the unit disc under star-like functions (cf. Star-like function).
Star-like domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Star-like_domain&oldid=32566