Liouville number
From Encyclopedia of Mathematics
A real number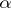 
such that for any 
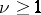the inequality
 |
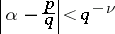has infinitely many integer solutions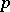 
and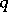 
satisfying the conditions 
, 
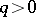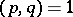. The fact that a Liouville number is transcendental (cf. Transcendental number) follows from the Liouville theorem (cf. Liouville theorems). These numbers were studied by J. Liouville [1].
Examples of Liouville numbers are:
 |
 |
 |
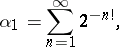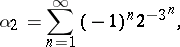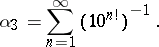References
| [1] | J. Liouville, "Sur des classes très étendues de quantités dont la valeur n'est ni algébrique, ni même réductible à des irrationelles algébriques" C.R. Acad. Sci. Paris , 18 (1844) pp. 883–885 |
| [2] | A.O. Gel'fond, "Transcendental and algebraic numbers" , Dover, reprint (1960) (Translated from Russian) |
Comments
References
| [a1] | O. Perron, "Die Lehre von den Kettenbrüchen" , 1 , Teubner (1977) pp. Sect. 35 |
| [a2] | O. Perron, "Irrationalzahlen" , Chelsea, reprint (1948) |
How to Cite This Entry:
Liouville number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Liouville_number&oldid=32555
Liouville number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Liouville_number&oldid=32555
This article was adapted from an original article by S.V. Kotov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article