Hyperbolic spiral
From Encyclopedia of Mathematics
A plane transcendental curve whose equation in polar coordinates is
 |
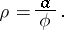It consists of two branches, which are symmetric with respect to a straight line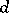 
(see Fig.). The pole is an asymptotic point. The asymptote is the straight line parallel to the polar axis at a distance 
from it. The arc length between two points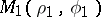 
and 
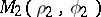is
 |
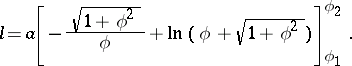The area of the sector bounded by an arc of the hyperbolic spiral and the two radius vectors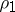 
and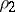 
corresponding to the angles 
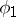and 
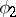is
 |
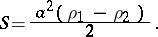A hyperbolic spiral and an Archimedean spiral may be obtained from each other by inversion with respect to the pole 
of the hyperbolic spiral.
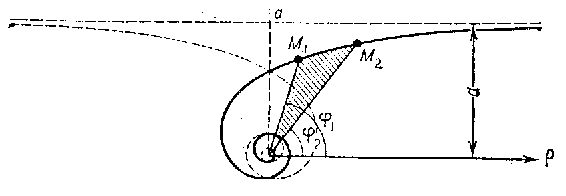
Figure: h048340a
A hyperbolic spiral is a special case of the so-called algebraic spirals.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
How to Cite This Entry:
Hyperbolic spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_spiral&oldid=32543
Hyperbolic spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_spiral&oldid=32543
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article