Archimedean spiral

A plane transcendental curve the equation of which in polar coordinates has the form:

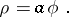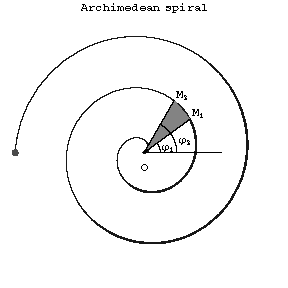
Figure: a013150a

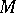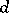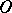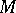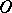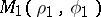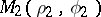It is described by a point moving at a constant rate along a straight line that rotates around a point lying on that straight line. At the starting point of the motion, coincides with the centre of rotation of the straight line (see Fig.). The length of the arc between the points and is

The area of the sector bounded by an arc of the Archimedean spiral and two radius vectors 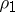and 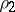, corresponding to angles 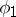and , is

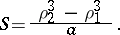An Archimedean spiral is a so-called algebraic spiral (cf. Spirals). The generalization of the Archimedean spiral is called a neoid, the equation of which in polar coordinates is

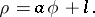The spiral was studied by Archimedes (3rd century B.C.) and was named after him.

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)

References

[a1]	E.H. Lockwood, "A book of curves" , Cambridge Univ. Press (1961)