Almost-period

A concept from the theory of almost-periodic functions (cf. Almost-periodic function); a generalization of the notion of a period. For a uniformly almost-periodic function , , 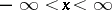a number is called an -almost-period of if for all ,

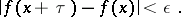For generalized almost-periodic functions the concept of an almost-period is more complicated. For example, in the space an -almost-period is defined by the inequality

where 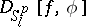is the distance between 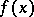and 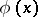in the metric of .

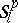A set of almost-periods of a function 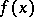is said to be relatively dense if there is a number 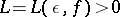such that every interval 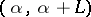of the real line contains at least one number from this set. The concepts of uniformly almost-periodic functions and that of Stepanov almost-periodic functions may be defined by requiring the existence of relatively-dense sets of -almost-periods for these functions.

References

[1]	B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian)

Comments

For the definition of 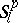and its metric 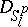see Almost-periodic function. The Weyl, Besicovitch and Levitan almost-periodic functions can also be characterized in terms of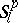 -periods. These characterizations are more complicated. A good additional reference is [a1], especially Chapt. II.

References

[a1]	A.S. Besicovitch, "Almost periodic functions" , Cambridge Univ. Press (1932)