Maximal subgroup
From Encyclopedia of Mathematics
A proper subgroup of a group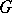 
which is not contained in any other proper subgroup of 
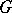, that is, a maximal element in the set of proper subgroups of 
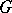ordered by inclusion. There exist groups without maximal subgroups, for example, a group of type 
.
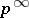A generalization of the concept of a maximal subgroup is that of a subgroup maximal with respect to some property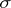 
, i.e. a subgroup 
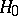of 
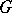with the property 
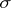and such that no other proper subgroup 
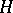of 
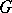has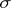 
and contains 
.
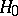References
| [1] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) |
Comments
A proper subgroup of a group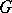 
is a subgroup 
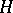of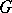 
satisfying 
.
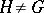References
| [a1] | M. Hall jr., "The theory of groups" , Macmillan (1959) |
How to Cite This Entry:
Maximal subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_subgroup&oldid=32492
Maximal subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_subgroup&oldid=32492
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article