Convergence multipliers
From Encyclopedia of Mathematics
for a series 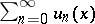 of functions
of functions
Numbers 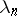 ,
, 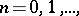 such that the series
such that the series 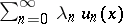 converges almost-everywhere on a measurable set
converges almost-everywhere on a measurable set 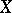 , where the
, where the 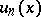 are numerical functions defined on
are numerical functions defined on 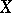 .
.
For example, for the trigonometric Fourier series of a function from 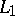 , the numbers
, the numbers 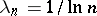 ,
, 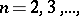 are convergence multipliers (
are convergence multipliers (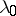 and
and 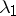 can be chosen arbitrarily), i.e. if
can be chosen arbitrarily), i.e. if 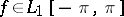 and if
and if
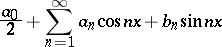 |
is its trigonometric Fourier series, then the series
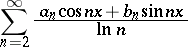 |
converges almost-everywhere on the whole real line. If 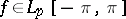 ,
, 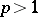 , then its trigonometric Fourier series itself converges almost-everywhere (see Carleson theorem).
, then its trigonometric Fourier series itself converges almost-everywhere (see Carleson theorem).
How to Cite This Entry:
Convergence multipliers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence_multipliers&oldid=32486
Convergence multipliers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence_multipliers&oldid=32486
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article