Quasi-uniform convergence
From Encyclopedia of Mathematics
A generalization of uniform convergence. A sequence of mappings 
from a topological space 
into a metric space 
converging pointwise to a mapping 
is called quasi-uniformly convergent if for any 
and any positive integer 
there exist a countable open covering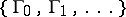 
of 
and a sequence 
of positive integers greater than 
such that 
for every 
. Uniform convergence implies quasi-uniform convergence. For sequences of continuous functions, quasi-uniform convergence is a necessary and sufficient condition for the limit function to be continuous (the Arzelà–Aleksandrov theorem).
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
How to Cite This Entry:
Quasi-uniform convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-uniform_convergence&oldid=32477
Quasi-uniform convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-uniform_convergence&oldid=32477
This article was adapted from an original article by V.V. Fedorchuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article