Galois topological group
A Galois group endowed with the Krull topology; the filter base (i.e. a basis of the open neighbourhoods of the identity) of this topology consists of normal subgroups of finite index. If 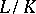 is a finite Galois extension, the topology of its Galois group
is a finite Galois extension, the topology of its Galois group 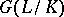 is discrete. If the field
is discrete. If the field 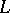 is the union of finite Galois extensions
is the union of finite Galois extensions 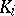 of a field
of a field 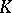 , the (topological) Galois group
, the (topological) Galois group 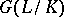 is the projective limit of the finite groups
is the projective limit of the finite groups 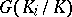 where each of the
where each of the 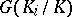 is given the discrete topology, and is a profinite group, hence a totally-disconnected compact topological group. If
is given the discrete topology, and is a profinite group, hence a totally-disconnected compact topological group. If 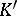 is the field of invariants for
is the field of invariants for 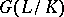 , the subgroup
, the subgroup 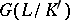 is everywhere dense in
is everywhere dense in 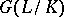 . The main theorem on finite Galois extensions may be generalized to infinite extensions: There is a one-to-one correspondence between the closed subgroups of the topological Galois group of a Galois extension
. The main theorem on finite Galois extensions may be generalized to infinite extensions: There is a one-to-one correspondence between the closed subgroups of the topological Galois group of a Galois extension 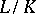 and the subfields of
and the subfields of 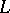 containing
containing 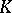 .
.
Comments
Open subgroups of  correspond to subfields of
correspond to subfields of  that have finite degree over
that have finite degree over 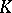 . If
. If  is an arbitrary subgroup of
is an arbitrary subgroup of 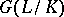 , then the extension
, then the extension 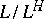 is Galois (cf. Galois extension), and
is Galois (cf. Galois extension), and 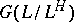 is the closure of
is the closure of 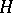 .
.
Galois topological group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_topological_group&oldid=32456