Fatou arc
for a meromorphic function  in a domain
in a domain  of the complex
of the complex  -plane
-plane
An accessible boundary arc (cf. Attainable boundary arc) of  with the property that it forms part of the boundary of some Jordan domain
with the property that it forms part of the boundary of some Jordan domain  in which
in which  ,
,  , is bounded. Sometimes this definition is broadened, replacing the condition that
, is bounded. Sometimes this definition is broadened, replacing the condition that  is bounded in
is bounded in  by the more general condition that the image of
by the more general condition that the image of  under the mapping
under the mapping 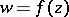 is not dense in the
is not dense in the 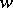 -plane. The strengthened version of Fatou's theorem in the theory of boundary properties of analytic functions asserts that if
-plane. The strengthened version of Fatou's theorem in the theory of boundary properties of analytic functions asserts that if  is a Fatou arc (even in the extended sense) for a function
is a Fatou arc (even in the extended sense) for a function  that is meromorphic in the disc
that is meromorphic in the disc 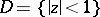 , then at almost-every point
, then at almost-every point  ,
,  has a finite limit as
has a finite limit as  tends to
tends to  from inside
from inside 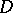 within any angle with vertex
within any angle with vertex  formed by a pair of chords of
formed by a pair of chords of 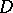 .
.
References
| [1] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Fatou arc. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fatou_arc&oldid=32435