Splitting field of a polynomial
The smallest field containing all roots of that polynomial. More exactly, an extension  of a field
of a field  is called the splitting field of a polynomial
is called the splitting field of a polynomial  over the field
over the field  if
if  decomposes over
decomposes over  into linear factors:
into linear factors:
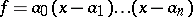 |
and if  (see Extension of a field). A splitting field exists for any polynomial
(see Extension of a field). A splitting field exists for any polynomial  , and it is defined uniquely up to an isomorphism that is the identity on
, and it is defined uniquely up to an isomorphism that is the identity on 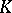 . It follows from the definition that a splitting field is a finite algebraic extension of
. It follows from the definition that a splitting field is a finite algebraic extension of 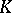 .
.
Examples. The field of complex numbers 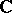 serves as the splitting field of the polynomial
serves as the splitting field of the polynomial  over the field
over the field 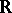 of real numbers. Any finite field
of real numbers. Any finite field  , where
, where 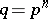 , is the splitting field of the polynomial
, is the splitting field of the polynomial 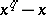 over the prime subfield
over the prime subfield 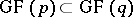 .
.
Comments
See also Galois theory; Irreducible polynomial.
References
| [a1] | I. Stewart, "Galois theory" , Chapman & Hall (1979) |
Splitting field of a polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Splitting_field_of_a_polynomial&oldid=32434