Verbal product
From Encyclopedia of Mathematics
of groups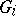 
, 
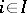
The quotient group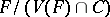 
, where 
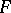is the free product of the groups 
, 
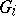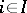(cf. Free product of groups), 
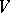is some set of words, 
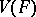is the verbal 
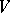-subgroup (cf. Verbal subgroup) of 
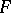, and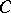 
is the Cartesian subgroup (i.e. the kernel of the natural epimorphism of 
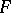onto the direct product of these groups). As an operation on a class of groups, the verbal product is associative and, within the corresponding variety of groups, it is also free.
Comments
References
| [a1] | W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations in terms of generators and relations" , Wiley (Interscience) (1966) pp. 412 |
How to Cite This Entry:
Verbal product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Verbal_product&oldid=32423
Verbal product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Verbal_product&oldid=32423
This article was adapted from an original article by O.N. Golovin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article