Totally-imperfect space
From Encyclopedia of Mathematics
A topological space not containing a subset homeomorphic to a Cantor set. For instance, any complete separable uncountable metrizable space contains an uncountable subspace that, as well as its complement, is totally imperfect.
Comments
A subset of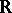 
such that it and its complement are totally imperfect is usually called a Bernstein set, after F. Bernstein [a1]. Such sets are non-measurable.
References
| [a1] | F. Bernstein, "Zur Theorie der trigonometrischen Reihe" Ber. K. Sächs. Ges. Wissenschaft. Leipzig Math.-Phys. Kl. , 60 (1908) pp. 325–338 |
How to Cite This Entry:
Totally-imperfect space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Totally-imperfect_space&oldid=32380
Totally-imperfect space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Totally-imperfect_space&oldid=32380
This article was adapted from an original article by A.A. Mal'tsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article