Semi-bounded operator
From Encyclopedia of Mathematics
A symmetric operator 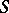 on a Hilbert space
on a Hilbert space 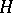 for which there exists a number
for which there exists a number  such that
such that
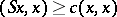 |
for all vectors  in the domain of definition of
in the domain of definition of 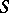 . A semi-bounded operator
. A semi-bounded operator 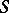 always has a semi-bounded self-adjoint extension
always has a semi-bounded self-adjoint extension  with the same lower bound
with the same lower bound  (Friedrichs' theorem). In particular,
(Friedrichs' theorem). In particular, 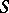 and its extension have the same deficiency indices (cf. Defective value).
and its extension have the same deficiency indices (cf. Defective value).
References
| [1] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
How to Cite This Entry:
Semi-bounded operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-bounded_operator&oldid=32353
Semi-bounded operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-bounded_operator&oldid=32353
This article was adapted from an original article by V.I. Lomonosov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article