Bertrand curves
From Encyclopedia of Mathematics
conjugate curves, Bertrand pair
Two space curves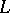 
and 
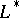with common principal normals. Let 
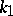and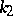 
be the curvature and the torsion of 
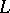respectively. For the curves 
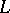and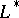 
to be conjugate it is necessary and sufficient that
 |
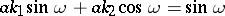is true. Here 
is a constant, and 
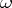is the angle between the tangent vectors of 
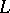and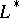 
. The name Bertrand curve is also given to a curve 
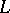for which there exists a conjugate curve 
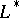. They were introduced by J. Bertrand in 1850.
Comments
Bertrand's original paper is [a2]. A general reference is [a1].
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
| [a2] | J. Bertrand, "Mémoire sur la théorie des courbes à double courbure" Liouvilles Journal , 15 (1850) |
How to Cite This Entry:
Bertrand curves. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bertrand_curves&oldid=32346
Bertrand curves. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bertrand_curves&oldid=32346
This article was adapted from an original article by E.V. Shikin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article