First integral
of an ordinary differential equation
A non-constant continuously-differentiable function whose derivative vanishes identically on the solutions of that equation. For a scalar equation
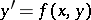 | (*) |
a first integral is a function  which occurs in the general solution
which occurs in the general solution  , where
, where  is an arbitrary constant. Therefore,
is an arbitrary constant. Therefore,  satisfies the linear equation
satisfies the linear equation
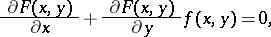 |
containing first-order partial derivatives. A first integral need not exist throughout the domain of definition of (*), but it always exists in a small region around a point at which  is continuously differentiable. A first integral is not uniquely defined. For example, for the equation
is continuously differentiable. A first integral is not uniquely defined. For example, for the equation  , a first integral is not only
, a first integral is not only  but also, e.g.,
but also, e.g., 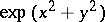 .
.
Knowledge of a first integral for a normal system
 |
enables one to reduce the order of this system by one, while the search for  functionally-independent first integrals is equivalent to the search for the general solution in implicit form. If
functionally-independent first integrals is equivalent to the search for the general solution in implicit form. If 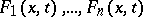 are functionally-independent first integrals, then any other first integral
are functionally-independent first integrals, then any other first integral 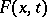 can be put in the form
can be put in the form
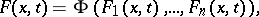 |
where 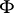 is some differentiable function.
is some differentiable function.
References
| [1] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
First integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=First_integral&oldid=32333