Indicatrix of tangents
From Encyclopedia of Mathematics
of a curve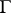 
in a Euclidean space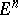 
The curve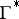 
on the sphere 
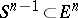which assigns to the parameter value 
the point whose position vector is parallel to the tangent vectors at 
to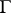 
. In order that a spherical curve 
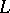be the indicatrix of tangents of some closed curve in 
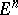it is necessary and sufficient that 
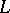is not confined to some open half-sphere (Krein's theorem).
References
| [1] | M.Ya. Vygodskii, "Differential geometry" , Moscow-Leningrad (1949) (In Russian) |
Comments
The indicatrix of tangents is also called the spherical tangent image. See also Spherical indicatrix.
How to Cite This Entry:
Indicatrix of tangents. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Indicatrix_of_tangents&oldid=32312
Indicatrix of tangents. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Indicatrix_of_tangents&oldid=32312
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article