Y-system
 -system,
-system, 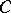 -system
-system
A smooth dynamical system (a flow (continuous-time dynamical system) or cascade) with a compact phase manifold, which is a hyperbolic set. A diffeomorphism generating a 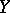 -cascade is called a
-cascade is called a 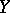 -diffeomorphism.
-diffeomorphism. 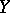 -systems were introduced by D.V. Anosov (see , [2]), and they are often called Anosov systems.
-systems were introduced by D.V. Anosov (see , [2]), and they are often called Anosov systems.
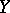 -systems are structurally stable (cf. Rough system), and a small (in the sense of
-systems are structurally stable (cf. Rough system), and a small (in the sense of 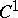 ) perturbation of a
) perturbation of a 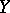 -system is again a
-system is again a 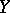 -system. The number of periodic trajectories of a
-system. The number of periodic trajectories of a 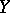 -system of period at most
-system of period at most 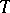 increases exponentially with
increases exponentially with 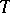 .
. 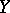 -systems possess strong ergodic properties with respect to the wide class of so-called "Gibbs" invariant measures (see [4]–[6]). In particular, if a
-systems possess strong ergodic properties with respect to the wide class of so-called "Gibbs" invariant measures (see [4]–[6]). In particular, if a 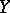 -system has a finite invariant measure "compatible with the smoothness" , that is, defined in terms of local coordinates by a positive density (in the early papers, only measures of this type were considered: see –[3]), then it must be a Gibbs measure. Thus, if a
-system has a finite invariant measure "compatible with the smoothness" , that is, defined in terms of local coordinates by a positive density (in the early papers, only measures of this type were considered: see –[3]), then it must be a Gibbs measure. Thus, if a 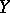 -diffeomorphism does not have wandering points (cf. Wandering point), then it is metrically isomorphic to a Bernoulli automorphism: under broad assumptions the convergence of the time averages to the space average is subject to the central limit theorem, and the rate of intermixing is exponential ( "exponential decay of correlations" ).
-diffeomorphism does not have wandering points (cf. Wandering point), then it is metrically isomorphic to a Bernoulli automorphism: under broad assumptions the convergence of the time averages to the space average is subject to the central limit theorem, and the rate of intermixing is exponential ( "exponential decay of correlations" ).
In the investigation of 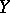 -systems, frequent use is made of symbolic dynamics, which became possible due to the Markov partitions introduced in [7], [8] (the definitive version is in [5], cf. also Symbolic dynamics). A number of results about
-systems, frequent use is made of symbolic dynamics, which became possible due to the Markov partitions introduced in [7], [8] (the definitive version is in [5], cf. also Symbolic dynamics). A number of results about 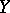 -systems have been proved to hold also for certain other types of hyperbolic sets. There are also less direct generalizations, in which the conditions of hyperbolicity are weakened slightly (see [6], ).
-systems have been proved to hold also for certain other types of hyperbolic sets. There are also less direct generalizations, in which the conditions of hyperbolicity are weakened slightly (see [6], ).
Hyperbolic automorphisms of tori and geodesic flows (cf. Geodesic flow) on closed manifolds of negative curvature are 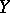 -systems. There are also other examples of a related algebraic-geometric nature. In these examples, the
-systems. There are also other examples of a related algebraic-geometric nature. In these examples, the 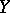 -system has an invariant measure compatible with the smoothness. By a small perturbation, such a measure can disappear, but in view of the structural stability all points remain non-wandering. Examples of
-system has an invariant measure compatible with the smoothness. By a small perturbation, such a measure can disappear, but in view of the structural stability all points remain non-wandering. Examples of 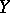 -systems with wandering points (see [9]) are of a fundamentally different character.
-systems with wandering points (see [9]) are of a fundamentally different character.
The existence of a 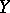 -system on a manifold imposes restrictions on the topological properties of the manifold. Little is known about this in general (see [10], [11]), but the case when the stable or unstable manifold (see Hyperbolic set) is one-dimensional has been investigated thoroughly (see [9], , [13], [15]).
-system on a manifold imposes restrictions on the topological properties of the manifold. Little is known about this in general (see [10], [11]), but the case when the stable or unstable manifold (see Hyperbolic set) is one-dimensional has been investigated thoroughly (see [9], , [13], [15]).
References
| [1a] | D.V. Anosov, "Roughness of geodesic flows on compact Riemannian manifolds of negative curvature" Soviet Math. Dokl. , 3 (1962) pp. 1068–1069 Dokl. Akad. Nauk SSSR , 145 : 4 (1962) pp. 707–709 |
| [1b] | D.V. Anosov, "Ergodic properties of geodesic flows on closed Riemannian manifolds of negative curvature" Soviet Math. Dokl. , 4 (1963) pp. 1153–1156 Dokl. Akad. Nauk SSSR , 151 : 6 (1963) pp. 1250–1252 |
| [2] | D.V. Anosov, "Geodesic flows on closed Riemann manifolds of negative curvature" Proc. Steklov Inst. Math. , 90 (1969) Trudy Mat. Inst. Steklov. , 90 (1967) |
| [3] | D.V. Anosov, "Some smooth ergodic systems" Russian Math. Surveys , 22 : 5 (1967) pp. 103–167 Uspekhi Mat. Nauk. , 22 : 5 (1967) pp. 107–172 |
| [4] | Ya.G. Sinai, "Gibbs measures in ergodic theory" Russian Math. Surveys , 27 : 4 (1972) pp. 21–64 Uspekhi Mat. Nauk. |
| [5] | R. Bowen, "Equilibrium states and the ergodic theory of Anosov diffeomorphisms" , Lect. notes in math. , 470 , Springer (1975) |
| [6] | A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 (1977) pp. 974–1065 Itogi Nauk. i Tekhn. Mat. Anal. , 13 (1975) pp. 129–262 |
| [7] | R.L. Adler, B. Weiss, "Similarity of automorphisms of the torus" Mem. Amer. Math. Soc. , 98 (1970) |
| [8] | Ya.G. Sinai, "Construction of Markov partitions" Funct. Anal. Appl. , 2 (1968) pp. 70–80 Funkts. Anal. i Prilozh. , 2 (1968) pp. 64–89 |
| [9] | J.M. Franks, B. Williams, "Anomalous Anosov flows" Z. Nitecki (ed.) C. Robinson (ed.) , Global theory of dynamical systems (Proc. Evanston, 1969) , Lect. notes in math. , 819 , Springer (1980) pp. 158–174 |
| [10] | M.W. Hirsch, "Anosov maps, polycyclic groups and homology" Topology , 10 : 3 (1971) pp. 177–183 |
| [11] | K. Shiraiwa, "Manifolds which do not admit Anosov diffeomorphisms" Nagoya Math. J. , 49 (1973) pp. 111–115 |
| [12a] | J.M. Franks, "Anosov diffeomorphisms" S.-S. Chern (ed.) S. Smale (ed.) , Global analysis , Proc. Symp. Pure Math. , 14 , Amer. Math. Soc. (1970) pp. 61–93 |
| [12b] | S.E. Newhouse, "On codimension one Anosov diffeomorphisms" Amer. J. Math. , 92 (1970) pp. 761–770 |
| [12c] | A. Manning, "There are no new Anosov diffeomorphisms on tori" Amer. J. Math. , 96 (1974) pp. 422–429 |
| [13] | A. Verjovsky, "Codimension one Anosov flows" Bolet. Soc. Mat. Mexicana , 19 : 2 (1974) pp. 49–77 |
| [14a] | A. Fahti, F. Laudenbach, "Les feuilletages mesurés" Astérisque , 66–67 (1979) pp. 71–126 |
| [14b] | A. Fahti, F. Laudenbach, "Comment Thurston compactifie l'espace de Teichmüller" Astérisque , 66–67 (1979) pp. 139–158 |
| [14c] | A. Fahti, V. Poénaru, "Theorème d'unicité des difféomorphismes pseudo-Anosov" Astérisque , 66–67 (1979) pp. 225–242 |
| [15] | V.V. Solodov, "Topological questions in the theory of dynamical systems" Russian Math. Surveys , 46 : 4 (1991) pp. 107–130 Uspekhi Mat. Nauk , 46 : 4 (1991) pp. 91–114 |
Comments
In Western literature the term Anosov system (-flow, -diffeomorphism) is consistently used. Anosov flows are particular cases of Axiom-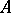 flows, i.e., flows on compact manifolds in which the set of non-wandering points (cf. Non-wandering point) is a hyperbolic set in which the periodic points (cf. Periodic point) are dense. Axiom-
flows, i.e., flows on compact manifolds in which the set of non-wandering points (cf. Non-wandering point) is a hyperbolic set in which the periodic points (cf. Periodic point) are dense. Axiom-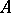 flows were introduced by S. Smale. Much information about Anosov systems can be found in [a2].
flows were introduced by S. Smale. Much information about Anosov systems can be found in [a2].
References
| [a1] | T. Adachi, "Distribution of closed orbits with a pre-assigned homology class in a negatively curved manifold" Nagoya Math. J. , 110 (1988) pp. 1–14 |
| [a2] | R. Bowen, "On Axiom 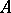 diffeomorphisms" , Amer. Math. Soc. (1978) diffeomorphisms" , Amer. Math. Soc. (1978) |
| [a3] | P. Eberlein, "When is a geodesic flow Anosov type?" J. Differential Geom. , 8 (1973) pp. 437–463 |
| [a4] | J.F. Plante, "Homology of closed orbits of Anosov flows" Proc. Amer. Math. Soc. , 37 (1973) pp. 297–300 |
| [a5] | M. Shub, "Global stability of dynamical systems" , Springer (1986) |
| [a6] | W. De Melo, "Geometric theory of dynamical systems" , Springer (1982) |
| [a7] | S. Smale, "Differentiable dynamical systems" Bull. Amer. Math. Soc. , 73 (1967) pp. 747–817 |
Y-system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Y-system&oldid=32282