Zorn lemma

maximal principle

If in a non-empty partially ordered set 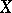every totally ordered subset (cf. Totally ordered set) has an upper bound, then 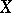contains a maximal element. An element 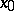is called an upper bound of a subset 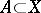if for all 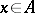. If an upper bound for 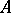exists, then the set 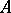is said to be bounded above. An element 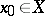is called maximal in 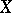if there is no element 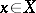, , 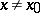such that .

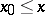The lemma was stated and proved by M. Zorn in [1]. It is equivalent to the axiom of choice.

References

[1]	M. Zorn, "A remark on a method in transfinite algebra" Bull. Amer. Math. Soc. , 41 (1935) pp. 667–670
[2]	J.L. Kelley, "General topology" , Springer (1975)

Comments

Earlier versions of the maximal principle, differing in detail from the one stated above but logically equivalent to it, were introduced independently by several mathematicians, the earliest being F. Hausdorff in 1909. For accounts of the history of the maximal principle, see [a1]–[a3].

References

[a1]	P.J. Campbell, "The origin of "Zorn's lemma" " Historia Math. , 5 (1978) pp. 77–89
[a2]	G.H. Moore, "Zermelo's axiom of choice" , Springer (1982)
[a3]	J. Rubin, H. Rubin, "Equivalents of the axiom of choice" , 1–2 , North-Holland (1963–1985)