Euler substitutions
Substitutions of the variable 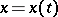 in an integral
in an integral
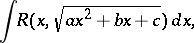 | (1) |
where 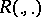 is a rational function of its arguments, that reduce (1) to the integral of a rational function. There are three types of such substitutions.
is a rational function of its arguments, that reduce (1) to the integral of a rational function. There are three types of such substitutions.
The first Euler substitution: If 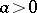 , then
, then
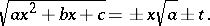 |
The second Euler substitution: If the roots 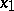 and
and 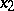 of the quadratic polynomial
of the quadratic polynomial 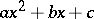 are real, then
are real, then
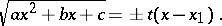 |
The third Euler substitution: If 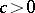 , then
, then
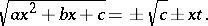 |
(Any combination of signs may be chosen on the right-hand side in each case.) All the Euler substitutions allow both the original variable of integration  and
and 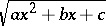 to be expressed rationally in terms of the new variable
to be expressed rationally in terms of the new variable 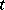 .
.
The first two Euler substitutions permit the reduction of (1) to the integral of a rational function over any interval on which 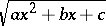 takes only real values.
takes only real values.
Geometrically, the Euler substitutions mean that the second-order curve
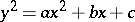 | (2) |
has a rational parametric representation; for if 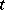 is chosen to be the angular coefficient of the pencil of straight lines
is chosen to be the angular coefficient of the pencil of straight lines 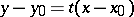 passing through a point
passing through a point 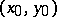 of (2), then the coordinates of any point on this curve can be expressed rationally in terms of
of (2), then the coordinates of any point on this curve can be expressed rationally in terms of 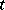 . In the case when
. In the case when 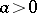 , that is, when (2) is a hyperbola, the first Euler substitution is obtained by taking as
, that is, when (2) is a hyperbola, the first Euler substitution is obtained by taking as 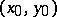 one of the points at infinity defined by the directions of the asymptotes of this hyperbola; when the roots
one of the points at infinity defined by the directions of the asymptotes of this hyperbola; when the roots 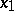 and
and 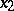 of the quadratic polynomial
of the quadratic polynomial 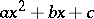 are real, the second Euler substitution is obtained by taking as
are real, the second Euler substitution is obtained by taking as 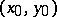 one of the points
one of the points 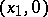 or
or 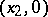 ; finally, when
; finally, when 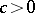 , the third Euler substitution is obtained by taking as
, the third Euler substitution is obtained by taking as 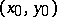 one of the points where the curve (2) intersects the ordinate axis, that is, one of the points
one of the points where the curve (2) intersects the ordinate axis, that is, one of the points 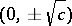 .
.
Euler substitutions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_substitutions&oldid=32131