Projective metric
A metric 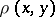 in a subset
in a subset 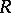 of a projective space
of a projective space 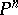 such that shortest paths with respect to this metric are parts of or entire projective straight lines. It is assumed that
such that shortest paths with respect to this metric are parts of or entire projective straight lines. It is assumed that 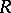 does not belong to a hypersurface and that: 1) for any three non-collinear points
does not belong to a hypersurface and that: 1) for any three non-collinear points  ,
, 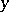 and
and  the triangle inequality holds in the strict sense:
the triangle inequality holds in the strict sense:
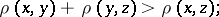 |
and 2) if 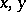 are different points in
are different points in 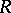 , then the intersection
, then the intersection 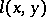 of the straight line
of the straight line 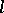 through
through  and
and 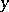 with
with 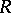 is either all of
is either all of 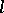 (a large circle), or is obtained from
(a large circle), or is obtained from 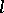 by discarding some segment (which may reduce to a point) (a metric straight line).
by discarding some segment (which may reduce to a point) (a metric straight line).
The set 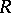 , provided with a projective metric, is called a projective-metric space.
, provided with a projective metric, is called a projective-metric space.
In one and the same projective-metric space there cannot exist simultaneously both types of straight lines: They are either all metric straight lines (i.e. isometric to an interval in 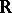 ), or they are all large circles of the same length (Hamel's theorem). Spaces of the first kind are called open (they coincide with subspaces of an affine space, i.e.
), or they are all large circles of the same length (Hamel's theorem). Spaces of the first kind are called open (they coincide with subspaces of an affine space, i.e. 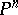 from which a hypersurface has been deleted); the geometry of open projective-metric spaces is also called Hilbert geometry. Spaces of the second kind are called closed (they coincide with the whole of
from which a hypersurface has been deleted); the geometry of open projective-metric spaces is also called Hilbert geometry. Spaces of the second kind are called closed (they coincide with the whole of 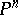 ).
).
The problem of determining all projective metrics is the so-called fourth problem of Hilbert (cf. [2]), and a complete solution of it was given by A.V. Pogorelov (1974).
The so-called projective determination of a metric is related to projective metrics, as a particular case. It consists of introducing in a subset of a projective space, by methods of projective geometry, a metric such that this subset becomes isomorphic to a Euclidean, elliptic or hyperbolic space. E.g., the geometry of open projective-metric spaces, whose subsets coincide with all of affine space, is called Minkowski geometry. Euclidean geometry is a Hilbert geometry and a Minkowski geometry simultaneously.
Hyperbolic geometry is a Hilbert geometry in which there exist reflections at all straight lines. The subset 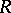 has a hyperbolic geometry if and only if it is the interior of an ellipsoid.
has a hyperbolic geometry if and only if it is the interior of an ellipsoid.
Elliptic geometry (or Riemann geometry) is the geometry of a projective-metric space of the second kind.
References
| [1] | P.J. Kelley, "Projective geometry and projective metrics" , Acad. Press (1953) |
| [2] | "Hilbert's problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German) |
Comments
References
| [a1] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
| [a2] | H. Busemann, "Metric methods in Finsler spaces and in the foundations of geometry" , Princeton Univ. Press (1942) |
Projective metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_metric&oldid=32094