Lie group, derived
From Encyclopedia of Mathematics
The commutator subgroup of a Lie group. For any Lie group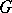 
its derived Lie group 
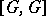is a normal (not necessarily closed) Lie subgroup of 
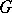. The corresponding ideal of the Lie algebra 
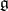of the group 
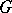coincides with the commutator algebra 
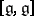(also called the derived Lie algebra of 
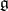). The commutator subgroup of a simply-connected (or connected linear) Lie group 
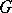is always closed in 
.
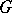References
| [1] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) |
How to Cite This Entry:
Lie group, derived. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_group,_derived&oldid=32088
Lie group, derived. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_group,_derived&oldid=32088
This article was adapted from an original article by A.L. Onishchik (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article