Translation surface

A surface formed by parallel displacement of a curve 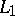in such a way that some point on it slides along another curve . If and are the position vectors of and , respectively, then the position vector of the translation surface is

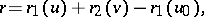where is the position vector of . The lines 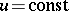and form a transport net. Each ruled surface has 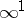transport nets (Reidemeister's theorem), while an enveloping translation surface can be only a cylinder or a plane. If a surface has two transport nets, then the non-singular points of the tangents of the lines in these nets lie on an algebraic curve of order four. An invariant feature of a translation surface is the existence of a conjugate Chebyshev net (a transport net). For example, an isotropic net on a minimal surface is a transport net, thus that surface is a translation surface. One may also characterize a translation surface by the fact that one of its curves (transport lines) passes into a line lying on the same surface as a result of the action of a one-parameter group of parallel displacements. Replacing this group by an arbitrary one-parameter group leads to generalized translation surfaces [1].

References

[1]	V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian)

References

[a1]	G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1–4 , Chelsea, reprint (1972) pp. Sects. 81–84; 218
[a2]	W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Affine Differentialgeometrie" , 2 , Springer (1923)
[a3]	W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Affine Differentialgeometrie" , 3 , Springer (1930)
[a4]	D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 103; 109; 184