Area function
From Encyclopedia of Mathematics
The set function on a sphere 
equal to the area 
of that part of the convex surface 
that has spherical image 
. This definition remains meaningful for general convex surfaces and it gives a totally-additive set function on the ring of Borel sets.
References
| [1] | A.D. Aleksandrov, Mat. Sb. , 3 : 1 (1938) pp. 27–44 |
| [2] | H. Busemann, "Convex surfaces" , Interscience (1958) |
Comments
In the article, 
is the unit sphere in 
with centre at the origin. If one associates to each point 
the unit normal vector 
and shifts this vector 
so that its base coincides with the origin, then the end point of 
is a point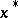 
on 
. The point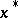 
is called the spherical image of 
. The procedure for obtaining the spherical image of a point goes under the name of spherical mapping, cf. Spherical map.
How to Cite This Entry:
Area function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Area_function&oldid=32073
Area function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Area_function&oldid=32073
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article