Sylow theorems
Three theorems on maximal  -subgroups in a finite group, proved by L. Sylow [1] and playing a major role in the theory of finite groups. Sometimes the union of all three theorems is called Sylow's theorem.
-subgroups in a finite group, proved by L. Sylow [1] and playing a major role in the theory of finite groups. Sometimes the union of all three theorems is called Sylow's theorem.
Let  be a finite group of order
be a finite group of order  , where
, where  is a prime number not dividing
is a prime number not dividing  . Then the following theorems hold.
. Then the following theorems hold.
Sylow's first theorem:  contains subgroups of order
contains subgroups of order  for all
for all  ; moreover, each subgroup of order
; moreover, each subgroup of order  is a normal subgroup in at least one subgroup of order
is a normal subgroup in at least one subgroup of order 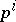 . This theorem implies, in particular, the following important results: there is in
. This theorem implies, in particular, the following important results: there is in 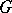 a Sylow subgroup of order
a Sylow subgroup of order  ; any
; any 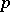 -subgroup of
-subgroup of 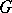 is contained in some Sylow
is contained in some Sylow 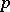 -subgroup of order
-subgroup of order  ; the index of a Sylow
; the index of a Sylow  -subgroup is not divisible by
-subgroup is not divisible by 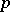 ; if
; if 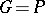 is a group of order
is a group of order 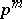 , then any of its proper subgroups is contained in some maximal subgroup of order
, then any of its proper subgroups is contained in some maximal subgroup of order 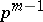 and all maximal subgroups of
and all maximal subgroups of 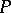 are normal.
are normal.
Sylow's second theorem: All Sylow  -subgroups of a finite group are conjugate.
-subgroups of a finite group are conjugate.
For infinite groups the analogous result is, in general, false.
Sylow's third theorem: The number of Sylow 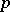 -subgroups of a finite group divides the order of the group and is congruent to one modulo
-subgroups of a finite group divides the order of the group and is congruent to one modulo 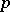 .
.
For arbitrary sets 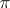 of prime numbers, analogous theorems have been obtained only for finite solvable groups (see Hall subgroup). For non-solvable groups the situation is different. For example, in the alternating group
of prime numbers, analogous theorems have been obtained only for finite solvable groups (see Hall subgroup). For non-solvable groups the situation is different. For example, in the alternating group 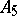 of degree 5, for
of degree 5, for 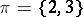 there is a Sylow
there is a Sylow 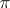 -subgroup
-subgroup 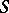 of order 6 whose index is divisible by a number from
of order 6 whose index is divisible by a number from  . In addition, in
. In addition, in  there is a Sylow
there is a Sylow 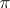 -subgroup isomorphic to
-subgroup isomorphic to 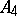 and not conjugate with
and not conjugate with 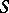 . The number of Sylow
. The number of Sylow  -subgroups in
-subgroups in 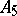 does not divide the order of
does not divide the order of 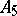 .
.
References
| [1] | L. Sylow, "Théorèmes sur les groupes de substitutions" Math. Ann. , 5 (1872) pp. 584–594 |
| [2] | M. Hall, "Group theory" , Macmillan (1959) |
Sylow theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sylow_theorems&oldid=32056