Heegaard decomposition

A representation of a closed three-dimensional manifold as a union of two three-dimensional submanifolds with a common boundary, each of which is a handle-body (that is, a three-dimensional ball with several handles of index 1). It was defined by P. Heegaard [1] in 1898. Heegaard decompositions are one of the most commonly used devices in the study of three-dimensional manifolds, although there are other more effective methods for decomposing three-dimensional manifolds into simple pieces (connected sums, hierarchies). Every closed three-dimensional manifold has a Heegaard decomposition. For the handle-bodies of the decomposition one may take, for example, a regular neighbourhood of the one-dimensional skeleton of a certain triangulation of the manifold and the closure of its complement. The genus (number of handles) of one handle-body is always the same as that of the other handle-body and is called the genus of the Heegaard decomposition. Two Heegaard decompositions of the same manifold 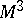are equivalent if the dividing surface (the common boundary of the handle-bodies) of one of them can be carried into that of the other by means of a certain homeomorphism of the manifold .

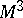References

[1]	P. Heegaard, "Sur l'analyse situs" Bull. Soc. Math. France , 44 (1916) pp. 161–242 (Translation of thesis (in Danish, 1898))