Conformal space

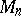
The Euclidean space 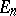extended by an ideal point (at infinity). It is considered in conformal geometry. The fundamental group corresponding to this space consists of point transformations taking spheres (circles in 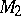) into spheres. By means of stereographic projection, the conformal space 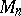is mapped onto the absolute 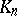of the space with a hyperbolic metric. The fundamental group of conformal geometry is isomorphic to the group of hyperbolic motions of this space .

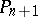The presence of the ideal point ensures that the stereographic projection is one-to-one. Under transformations of the conformal group, the ideal point can be taken to an ordinary point. Therefore, in a conformal space a sphere is indistinguishable from a plane: A plane is a sphere passing through the ideal point.

Comments

Conformal geometry is also called Möbius geometry, and the absolute of 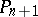is also called the absolute quadric of .

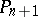More about the geometry of 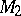can be found in [a1].

References

[a1]	H. Schwerdtfeger, "Geometry of complex numbers" , Dover, reprint (1979)