FC-group

finite conjugate group

A group 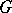such that each 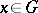has only finitely many conjugates. This is one of several important possible finiteness conditions on an (infinite) group (cf. also Group with a finiteness condition). FC-groups are similar to finite groups in several respects.

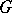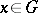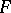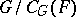Let be an arbitrary group. An element is an FC-element if it has only finitely many conjugates. The FC-elements form a characteristic subgroup , and is residually finite (here, 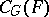is the centralizer of 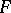in ).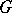

An FC-group is thus a group in which all elements are FC-elements.

The commutator subgroup of an FC-group is periodic (torsion).

A group 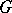is a finitely-generated FC-group if and only if it has a free Abelian subgroup 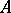of finite rank in its centre such that 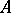is of finite index in .

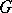For further results, see [a1], Part 1, Sect. 4.3; Part 2, pp. 102–104, and [a2], Sect. 15.1. See also CC-group.

References

[a1]	D.J.S. Robinson, "Finiteness conditions and generalized soluble groups, Parts 1–2" , Springer (1972)
[a2]	W.R. Scott, "Group theory" , Dover, reprint (1987)