Dandelin spheres

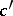Spheres forming part of the geometrical constructions relating the planimetric definition of the ellipse, hyperbola or parabola with their stereometric definitions. For instance, let two spheres (also known as Dandelin spheres), inscribed in a circular cone, make contact with the surface of the cone along circles and (see Fig.) and let 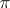be a certain plane passing through two points 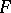and .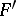

Figure: d030100a

If an arbitrary point 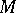is taken on the intersection line of the cone with 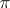, and a generatrix 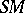is drawn intersecting and 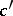, then if 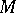varies, the points 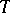and 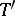move around the circles and 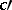while preserving the distance 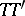, i.e. the intersection line will be an ellipse (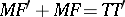, 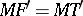and 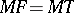). In the case of a hyperbola, Dandelin spheres are located in different sheets.

Suggested by G. Dandelin in 1822.

References

[1]	P.S. Modenov, "Analytic geometry" , Moscow (1969) (In Russian)

References

[a1]	M. Berger, "Geometry" , II , Springer (1987) pp. 227