Jung theorem

Every set of diameter in a Euclidean space is contained in a ball in 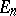of radius . There are analogues and generalizations of Jung's theorem (e.g. replacing the Euclidean distance by other metrics) (cf. [2]).

The theorem was proved by H.W.E. Jung [1].

References

[1]	H.W.E. Jung, "Ueber den kleinsten Kreis, der eine ebene Figur einschliesst" J. Reine Angew. Math. , 130 (1901) pp. 310–313
[2]	L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" V.L. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 101–180
[3]	H. Hadwiger, H. Debrunner, "Combinatorial geometry in the plane" , Holt, Rinehart & Winston (1964) (Translated from German)

Comments

The counterpart for inscribed balls is Steinhagen's theorem (cf. [a1]).

References

[a1]	T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1974)