Geodesic manifold
From Encyclopedia of Mathematics
at a point 
A submanifold 
of a smooth manifold 
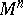(Riemannian or with an affine connection) such that the geodesic lines (cf. Geodesic line) of 
that are tangent to 
at 
have a contact of at least the second order with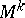 
. This requirement is fulfilled at all points if any geodesic in 
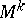is also a geodesic in 
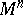. Such geodesic manifolds 
are called totally geodesic manifolds.
Comments
Also called geodesic submanifold and totally geodesic submanifold, respectively.
References
| [a1] | W. Klingenberg, "Riemannian geometry" , Springer (1982) (Translated from German) |
How to Cite This Entry:
Geodesic manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_manifold&oldid=31980
Geodesic manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_manifold&oldid=31980
This article was adapted from an original article by Yu.A. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article