Smooth continuum
From Encyclopedia of Mathematics
at a point 
A continuum 
such that for each sequence 
of points of 
converging towards a point 
and each subcontinuum 
containing 
and 
there exist a sequence of subcontinua 
in 
, 
, converging towards 
. A continuum that is smooth at each one of its points is called smooth.
Comments
Smoothness has a slightly different definition in the class of uniquely arcwise-connected continua, or dendroids (a continuum 
is uniquely arcwise-connected if for every 
and 
in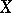 
there is a unique arc 
in 
connecting 
and 
). One calls a uniquely arcwise-connected continuum 
smooth if there is a 
such that 
whenever 
in 
. Such a point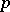 
is called an initial point of 
.
References
| [a1] | J.J. Charatonik, C. Eberhart, "On smooth dendroids" Fund. Math. , 67 (1970) pp. 297–322 |
How to Cite This Entry:
Smooth continuum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smooth_continuum&oldid=31974
Smooth continuum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smooth_continuum&oldid=31974
This article was adapted from an original article by A.A. Mal'tsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article