Osculating sphere
From Encyclopedia of Mathematics
at a point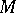 
of a curve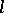 
The sphere having contact of order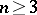 
with 
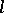at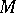 
(see Osculation). The osculating sphere can also be defined as the limit of a variable sphere passing through four points of 
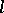as these points approach 
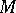. If the radius of curvature of 
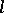at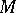 
is equal to 
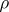and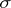 
is the torsion, then the formula for calculating the radius of the osculating sphere has the form
 |
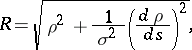where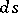 
denotes the differential along an arc of 
.
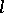Comments
References
| [a1] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1979) pp. 39 |
| [a2] | D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 25 |
How to Cite This Entry:
Osculating sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_sphere&oldid=31967
Osculating sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_sphere&oldid=31967
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article