Goursat congruence

A congruence of straight lines in which the first point invariant of the focal net of one focal surface is equal to the second point invariant of a second focal surface . Let 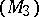, be the Laplace transforms (cf. Laplace transformation (in geometry)) of the focal surfaces 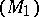and 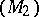. Then for each straight line 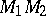of a Goursat congruence there exists a second-order surface passing through the points (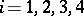) having a third-order osculation with the line on 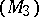and with the line on 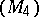[1]. If two adjacent congruences in a Laplace sequence are Goursat congruences, the complete sequence consists of Goursat congruences.

Named after E. Goursat, who studied congruences of this type.

References

[1]	G. Tzitzeica, "Sur certaines congruences de droites" J. Math. Pures Appl. (9) , 7 (1928) pp. 189–208
[2]	S.P. Finikov, "Projective differential geometry" , Moscow-Leningrad (1937) (In Russian)

Comments

Goursat congruences, which are rarely encountered anymore, can also be defined by the property that in their Laplace sequence both adjacent congruences have the same Laplace invariant [a1].

References

[a1]	G. Bol, "Projective Differentialgeometrie" , 2 , Vandenhoeck & Ruprecht (1954)