Quasi-compact space

A topological space 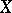in which every filter has at least one point of adherence. Equivalent to this condition are the following three: 1) every family of closed sets in 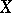with empty intersection contains a finite subfamily with empty intersection; 2) every ultrafilter in 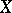is convergent; and 3) every open covering of 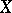contains a finite open subcovering of this space (the Borel–Lebesgue condition). A quasi-compact space is called compact (or 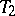-compact) if it is separated (or Hausdorff). For example, every space in which there are only a finite number of open sets is a quasi-compact space. In particular, any finite space is quasi-compact. A continuous image of a quasi-compact space is quasi-compact. A topological product of any number of quasi-compact spaces is quasi-compact (Tikhonov's theorem).

References

[1]	N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French)

Comments

Often a quasi-compact space is called compact and a space called compact here is explicitly called compact Hausdorff. See also Compact space.