Equicontinuity
From Encyclopedia of Mathematics
of a set of functions
An idea closely connected with the concept of compactness of a set of continuous functions. Let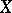 
and 
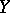be compact metric spaces and let 
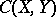be the set of continuous mappings of 
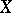into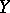 
. A set 
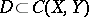is called equicontinuous if for any 
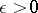there is a 
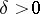such that 
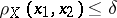implies 
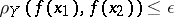for all 
, 
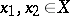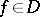. Equicontinuity of 
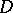is equivalent to the relative compactness of 
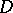in 
, equipped with the metric
 |
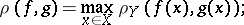this is the content of the Arzelà–Ascoli theorem. The idea of equicontinuity can be transferred to uniform spaces.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) |
Comments
References
| [a1] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1961) (Translated from French) |
How to Cite This Entry:
Equicontinuity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equicontinuity&oldid=31937
Equicontinuity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equicontinuity&oldid=31937
This article was adapted from an original article by E.M. Semenov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article